Sajtónyilvános eseményen, az újságírókkal közösen várta a fiziológiai és orvostudományi Nobel-díj bejelentését a Szegedi Tudományegyetem vezetősége 2023. október 2-án, az egyetem központi épületében. Az SZTE kutatóprofesszorát, Karikó Katalint évek óta az esélyesek között tartották számon, és idén meg is kapta a tudományos világ legjelentősebb elismerését. A Szegedi Tudományegyetem élőben kapcsolta az SZTE történetének második Nobel-díjasát, Amerikából.
Az SZTE oktatói, Bánhelyi Balázs, Csendes Tibor és Krisztin Tibor bécsi kollégájukkal, Arnold Neumaierrel E. M. Wright közel hatvan éves híres sejtését igazolták egy késleltetett differenciál-egyenlet megoldásainak konvergenciájáról. Ezért nekik ítélték oda az idei Moore-díjat a megbízható számítások terén.
Az SZTE három oktatójának valamint bécsi kutatótársuknak ítélte oda a Reliable Computing szerkesztőbizottsága a neves Moore Díjat egy közelmúltban megjelent cikkükért. A Szegedi Egyetem oktatói: Bánhelyi Balázs és Csendes Tibor informatikusok, és Krisztin Tibor matematikus bécsi kollégájukkal, Arnold Neumaier matematikussal 8 év munkájával igazolták E.M. Wright közel hatvan éves híres sejtését egy késleltetett differenciál-egyenlet megoldásainak konvergenciájáról. Eredményük az űrkutatásban, járványmodellezésben és pénzügyi folyamatok leírásában is hasznosítható. A cikk a SIAM Journal on Applied Dynamical Systems című vezető folyóiratban jelent meg két éve, ezt ismerte el most a rangos matematikai díjjal a Reliable Computing szerkesztőbizottsága.
A díjazott eredmény egyébként az utóbbi időben nagyobb érdeklődést kiváltó késleltetett differenciálegyenletekre vonatkozik. Ilyenek fordulnak elő irányítási feladatokban, például az űrutazás során, a fertőzések terjedése modellezésében, de pénzügyi folyamatok leírásában is.
 |
| Moore-díjasok (balról jobbra): Bánhelyi Balázs, Csendes Tibor és Krisztin Tibor, az SZTE oktatói. |
A díjazott eredmény azt igazolja, hogy egy viszonylag egyszerű késleltetett differenciálegyenlet, az u’(t) = -α u(t-1)[1+u(t)] megoldásai nullához tartanak. Ezt a tulajdonságot E. M. Wright 1955-ben igazolta az 0 < α < 37/24 paraméter tartományban, és bizonyíthatónak vélte az 1.567 értékig. Azt a sejtést mondta ki, hogy a tulajdonság érvényes π/2-ig.
A díjazott eredmény az eddig nyitott tartomány csaknem egészére, 1.5706-ig igazolta a sejtést (v.ö. π/2 ≈ 1.570796…). Az eredményhez új elméleti állítások és számítógépes futtatások egyaránt szükségesek voltak, ezek egyike nem lett volna elég kis előrelépéshez sem. Az algoritmusok fontos eleme volt az intervallum aritmetikán alapuló megbízható differenciálegyenlet megoldó. Ez tette lehetővé, hogy matematikai tétel bizonyítás erejű kijelentéseket lehessen tenni. Másrészt a szerzők sajnos belátták azt is, hogy a bemutatott módszertannal a π/2 nem érhető el, ehhez újabb elméleti fölismerés szükséges. Mivel ebben a pontban új jellegű megoldások is lehetségessé válnak (bifurkáció), ez várható volt.
 |
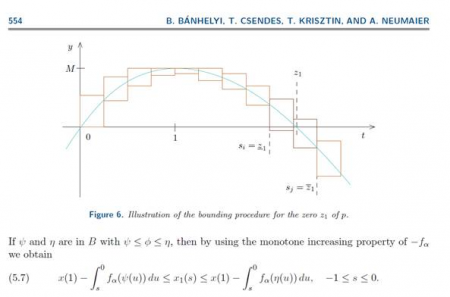| A díjazott eredmény az eddig nyitott tartomány csaknem egészére, 1.5706-ig igazolta a sejtést. |
A Reliable Computing szerkesztőbizottsága egyébként 2002-ben alapította a Moore-díjat, de magyar matematikusok, informatikusok munkáját most első alkalommal ismerték el a rangos díjjal, amelyet Svédországban, Uppsalában vehetnek át szeptemberben, a SCAN konferencián.
SZTEinfo
Fotó: Bobkó Anna
