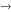Matematika mindenhol: a tomográfiát is ez működteti
Korong vagy gömb a Hold?
Matematika nélkül nem találta volna föl az emberiség például a modern orvostudomány „csodafegyverét”, a páciens belsejét térben is látni képes tomográfot. Kurusa Árpád matematikussal beszélgettünk.
 |
| Kurusa Árpád: Fizikai és térbeli problémák megoldását is lehetővé teszi a matematika. Fotók: Frank Yvette |
A fizika és az elektronika érdekelte igazán, mégis matematikus lett. Nem szeret rajzolni, mégis geometriával foglalkozik. Az ellentmondások eredményeként Kurusa Árpád, a Szegedi Tudományegyetem (SZTE) Természettudományi és Informatikai Kara Geometriai Tanszékét vezető egyetemi docens olyan matematikai problémákkal is foglalkozik, amelyek fizikai és térbeli problémák megoldását teszik lehetővé.
A Polygon és a tanárok. A tudományos eredmények megismertetését fontosnak tartja Kurusa Árpád. Ezért is lelkesedett a Polygon című, középiskolásoknak és középiskolai tanároknak szóló szegedi folyóiratuk alapításakor. Ott megjelentetett cikkeivel is tiszteleg egykori tanárai előtt, akiknek döntő szerepe volt Kurusa Árpád pályájának meghatározásában. Ságváris diákként Pintér Lajosné és Pintér Lajos, a legendás pedagógus házaspár hatására döntött a matematika mellett a fizika helyett. A szegedi egyetem matematika szakos hallgatójaként pedig az őt nagyon is érdeklő Csörgő Sándor-féle valószínűség számítás helyett a számára differenciálgeometriát tanító Szabó Zoltán javaslatára fordult az integrálgeometria irányába. Tudományága lényegét úgy magyarázza: ha valamely geometriai térben jelen lévő változó mennyiségű függvénynek csak valamilyen összegeit, vagyis integráljait ismerjük, akkor ezekből kellene mondani, hogy az a függvény hol mekkora és változásai észrevétlenek maradhatnak e? Ezzel foglalkozik az integrálgeometria.
– Bumerángtranszformáció. Ezzel a témával keresett meg Szabó Zoltán professzor negyedéves egyetemista koromban. Az ötletes név mögötti problémát úgy tudnám érzékeltetni, hogy képzeljük el: a levegő szennyezett, s mi szeretnénk megmérni ennek mértékét minden pontban úgy, hogy nem mozdulunk el a helyünkről. Elméletileg megtehetjük, hogy minden irányba és minden sebességgel eldobunk egy bumerángot, amelynek szennyeződését a levegőben megtett útja után méréssel állapítjuk meg. Vajon ezekből a mérési eredményekből ki lehet számolni a levegő szennyezettségét minden pontban? Erre kellett kigondolni egy formulát, valamiféle számolási módot – magyaráz lendületesen Kurusa Árpád, aki a problémára igazán szép megoldást talált, s eljutott a tomográfia matematikájáig. Egyik cikkében kifejtett eredményeit egy tomográfiai-eljárás szabadalmazásakor is fölhasználták.
A témát 1916–17 körül kezdték kutatni, ám a Funk és Radon nevéhez kötődő eredmények egyedi matematikai problémaként éltek egészen addig, amíg a magát orvos-fizikusnak nevező Cormack, aki ezért 1979-ben orvosi Nobel-díjat kapott, fel nem használta őket a röntgendiagnosztika forradalmasításához a tomográfiát létrehozó ötletében.. Cormack azt a kérdést fogalmazta meg, hogy ha készült egy csomó, például a fej egy-egy síkbeli szeletét mutató röntgenkép, akkor miért ne lehetne megmondani az alakját és helyét az agyban keresett daganatnak. A röntgenképen sötétebb folt mutatja a helyet, ahol a sűrűbb közegű szövet, például daganat elnyelte a röntgensugarat. Cormack a röntgenképek összekapcsolására használta föl a Radon-féle függvénytranszformációt: matematikai módszerrel térképezte föl a szövetek sűrűségét (persze a gyakorlatban ehhez számítógép kell, ezért is hívják ezeket a tomográfokat az angol kifejezés rövidítésével CAT-nek). Ez az az eljárás, amit ma tomográfiának, a modern orvostudomány egyik legújabb diagnosztikai csodafegyverének nevezünk. A tomográf anélkül képes a páciens fejébe látni, hogy annak bármilyen fizikai behatást el kellene viselnie.
– Csupa kérdés a matematikus élete – állítja Kurusa tanár úr. Példának gyerekkori történetet mesél. – Az Egri csillagokat olvasva gyerekkoromban eszembe jutott: miért fúrtak-kutattak a törökök az egri vár alaprajzát keresve, amikor elég lett volna körbejárniuk? Sok idő eltelt, mire rájöttem: vannak alakzatok, amelyek különböznek, holott minden körbejárásukról ugyanaz a kép mutatkozik. Például ha egy kört szemlélünk egy megfelelően – gyök kettőször – tágabb körívről, akkor minden egyes pontban 90 fokos szög alatt fog látszani. De ugyanez a helyzet, ha egy ellipszist a főköréről szemlélnék. Vagy: a „Sajtból van a Hold...” slágert hallva az vetődött fel bennem: honnan tudjuk, hogy gömb alakú a Hold, mikor a földről korongnak látjuk? Egy japán 1961-ben találta meg a matematikai bizonyítását: ha egy gömbön belül valami a gömbfelület minden pontjából gömbnek látszik, akkor az gömb is. Ha azonban annak a valaminek csak a fényességét tudnák a csillagászok mérni, akkor arra a kérdésre, hogy a minden pontból azonosan fénylő tárgy gömb vagy sem, mindmáig nem ismerjük a választ.
Újszászi Ilona
Forrás: delmagyar.hu