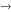„Buborék alakú, csupa üveg színház építhető-e?” A művészeti tervező és az építészmérnök kérdése nyitott maradt, ezért az acélszerkezetek és üvegtetők kivitelezésével is foglalkozó szegedi cég, az Alukonstrukt Kft. a Szegedi Tudományegyetem Természettudományi és Informatikai Kar Matematikai Tanszékcsoportjától, a Bolyai Intézettől kért tanácsot. Választ az Analízis Tanszék egyetemi docensétől, Makay Gézától kaptak: „Igen, de…”

– A pécsi konferenciaközpont betonépületei közé álmodott a művész egy üvegbuborékot, amelyben színházat, koncerttermet képzelt el – mutatja a számítógép-monitoron a nem szokványos terv vázlatát a matematikus. – Műszaki probléma, hogy a 9 méter magasságú és 25 méter hosszúságú, acélvázba illesztett üveglapokból álló épületnek el kell bírnia a saját súlyát, föl kell készülni – többek között – hóterhelésre, szélnyomásra, enyhe földmozgásra. Szerencsére ezekkel nekem nem kell foglalkoznom. Matematikusként az a feladatom, hogy ennek a vízcsepphez hasonlatos – nem szabályos gömb alakú – buborék felületnek olyan háromszögekre bontását adjam meg, amely már műszaki szempontból is elfogadható lehet. Vagyis meg kellett mondanom: hány darab és milyen méretű háromszögekből alakítható ki a buborékcsarnok.

Makay Géza: egy matematikai játék kiindulópontja lehet a gyakorlati alkalmazásnak is. Fotó: Frank Yvette

Egy fémrudakból összeállított háromszög önmagában merev, nem mozdul – szemben a négyszöggel. Ezért ezt a gömbszerű felületet megalkotása előtt háromszögekre kell bontani. Ám ezek élhossza 120–220 centiméter közötti lehet, a csúcspontoknál a fémmerevítőket tartó gumisablon 5 vagy 6 él befogadására képes – rögzítette a feltételt az Alukonstrukt Kft. Ez utóbbi a matematikus számára azt jelenti, hogy a buborékfelület belsejében a csúcsok ötöd- vagy hatodfokúak lehetnek, vagyis egy csúcsban 5 vagy 6 háromszög találkozhat. Az üvegben kialakuló belső feszültségre és a felület alátámaszthatóságára tekintettel pedig nem lehet nagyon hegyesszögű, illetve tompaszögű egyik háromszög sem. Figyelemmel kell lenni arra is, hogy a buborék külső palástján, a legnagyobb „kitüremkedésnél”, a föld fölött sétányt képzeltek el a látogatók számára.

– A szabályos gömb-, kúp- vagy hengerpalást tervezésére az építészek rendelkezésére áll szoftver, de erre a szabálytalan alakú buborékra nincs ilyen. Az egyedülálló probléma megoldása matematikai és programozási feladat. Ennek alaplépései: kitalálni az algoritmust, megalkotni a matematikai modellt, megírni a programot. Tavaly 9 hónapon át dolgoztam a buborékcsarnokon. Első ötletem a csúcsok egyenletes szétszórása volt a felületen, illetve ezek – matematikai kifejezéssel – konvex burka. Ám kiderült, hogy ez nem biztosítja a fenti ötöd-hatod fokúságot. Az Euler-féle poliédertétel alapján sikerült bebizonyítanom, hogy egy ilyen felületen legfeljebb 12 darab ötödfokú csúcs lehet. Ez mutatja, hogy ez a legmegszorítóbb feltétel – érzékelteti a felfedezés örömét Makay tanár úr. Végül egy olyan algoritmus vezetett eredményre, amely a felületet háromszögenként állítja össze, és közben betartja a fokszámokra adott feltételt is. Több háromszögelést is megkonstruál az általa készített program, hogy a kivitelező a megfelelő műszaki szempontok alapján választhassa ki a végsőt. Többségében 160–180 centiméter közötti élhosszúságú, összesen 500–800 háromszögből lesz megalkotható a buborékcsarnok. Közben megszületik a mindezt leíró cikk: egyik fejezete lesz az idén novemberben az Európai Unió által támogatott pályázat keretében megjelenő e-könyvnek, amely a matematika gyakorlati alkalmazásával foglalkozik majd.

Újszászi Ilona

forrás: delmagyar.hu